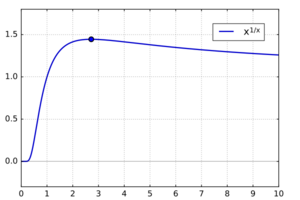
Steiner's calculus problem
Steiner's problem, asked and answered by (Steiner 1850), is the problem of finding the maximum of the function
- [math]\displaystyle{ f(x)=x^{1/x}.\, }[/math][1]
It is named after Jakob Steiner.
The maximum is at [math]\displaystyle{ x = e }[/math], where e denotes the base of the natural logarithm. One can determine that by solving the equivalent problem of maximizing
- [math]\displaystyle{ g(x) = \ln f(x) = \frac{\ln x}{x}. }[/math]
Applying the first derivative test, the derivative of [math]\displaystyle{ g }[/math] is
- [math]\displaystyle{ g'(x) = \frac{1-\ln x}{x^2}, }[/math]
so [math]\displaystyle{ g'(x) }[/math] is positive for [math]\displaystyle{ 0\lt x\lt e }[/math] and negative for [math]\displaystyle{ x\gt e }[/math], which implies that [math]\displaystyle{ g(x) }[/math] – and therefore [math]\displaystyle{ f(x) }[/math] – is increasing for [math]\displaystyle{ 0\lt x\lt e }[/math] and decreasing for [math]\displaystyle{ x\gt e. }[/math] Thus, [math]\displaystyle{ x=e }[/math] is the unique global maximum of [math]\displaystyle{ f(x). }[/math]
References
- ↑ Eric W. Weisstein. "Steiner's Problem". MathWorld. http://mathworld.wolfram.com/SteinersProblem.html. Retrieved December 8, 2010.
- Steiner, J. (1850), "Über das größte Product der Theile oder Summanden jeder Zahl", Crelle 40: 208, https://www.digizeitschriften.de/download/PPN243919689_0040/PPN243919689_0040___log28.pdf
 |